Use a recursion tree to give an asymptotically tight solution to the recurrence \(T(n) = T(\alpha n) +T((1-\alpha)n) + cn\), where \(\alpha\) is a constant in the range \(0 < \alpha < 1\) and \(c > 0\) is also a constant.
The recurrence \(T(n) = T(\alpha n) + T((1-\alpha)n) + cn\) has the following recursion tree:
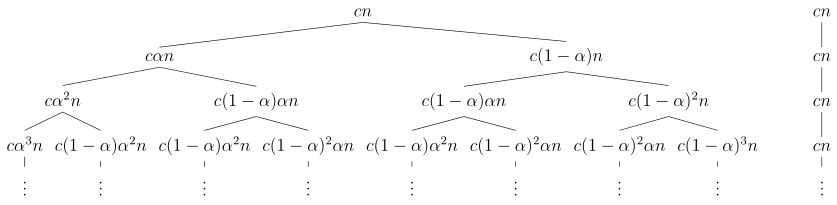
This tree is only complete until level \(\log_{1/(1-\alpha)}n\). Adding up the costs of each level of the tree:
\[\begin{split} T(n) &= \sum\limits_{i=0}^{\lg_{1/(1-\alpha)}n} cn \\ & = \left( \sum\limits_{i=1}^{\lg_{1/(1-\alpha)}n} cn \right) + cn \\ & = cn(\log_{1/(1-\alpha)}n) + cn \\ & = \Omega(n\log_{1/(1-\alpha)n}) \\ & = \Omega(n\lg n) \\ \end{split}\]We guess that \(T(n) \leq bn \lg n\). Substituting this into the recurrence yields
\[\begin{split} T(n) & \leq b \alpha n \lg(\alpha n) + b(1-\alpha)n \lg((1-\alpha)n) + cn \\ & = b \alpha n \lg \alpha + b \alpha n \lg n + b(1 - \alpha) n \lg (1 - \alpha) + b(1 - \alpha)n \lg n + cn \\ & = b \alpha n \lg \alpha + b \alpha n \lg n + b(1 - \alpha) n \lg (1 - \alpha) + bn \lg n - b \alpha \lg n + cn \\ & = bn \lg n + bn(\alpha \lg \alpha + (1 - \alpha) \lg(1 - \alpha)) + cn \\ & \leq bn \lg n \\ \end{split}\]Where the last step holds as long as \(b(\alpha \lg \alpha + (1 - \alpha) \lg (1 - \alpha)) + c \leq 0\). This bound looks pretty good, so let’s guess that our lower bound is \(T(n) \geq bn \lg n\). Substituting this into the reccurence yields
\[\begin{split} T(n) & \geq b \alpha n \lg(\alpha n) + b(1-\alpha)n \lg((1-\alpha)n) + cn \\ & = b \alpha n \lg \alpha + b \alpha n \lg n + b(1 - \alpha) n \lg (1 - \alpha) + b(1 - \alpha)n \lg n + cn \\ & = b \alpha n \lg \alpha + b \alpha n \lg n + b(1 - \alpha) n \lg (1 - \alpha) + bn \lg n - b \alpha \lg n + cn \\ & = bn \lg n + bn(\alpha \lg \alpha + (1 - \alpha) \lg(1 - \alpha)) + cn \\ & \geq bn \lg n \\ \end{split}\]Where the last step holds as long as \(b(\alpha \lg \alpha + (1 - \alpha) \lg (1 - \alpha)) + c \geq 0\). Therefore \(T(n) = \Theta(n \lg n)\).
The following LaTeX code was used to generate the above recursion tree:
\documentclass[12pt]{article}
\usepackage{forest}
\usepackage{tikz-qtree}
\begin{document}
\begin{figure}
\begin{minipage}[b]{0.5\linewidth}
\centering
\begin{tikzpicture}[scale=.75,sibling distance=0pt]
\Tree [.$cn$
[.$c\alpha n$
[.$c\alpha^2n$
[.$c\alpha^3n$
[.$\vdots$ ] ]
[.$c(1-\alpha)\alpha^2n$
[.$\vdots$ ] ] ]
[.$c(1-\alpha)\alpha n$
[.$c(1-\alpha)\alpha^2n$
[.$\vdots$ ] ]
[.$c(1-\alpha)^2\alpha n$
[.$\vdots$ ] ] ] ]
[.$c(1-\alpha)n$
[.$c(1-\alpha)\alpha n$
[.$c(1-\alpha)\alpha^2n$
[.$\vdots$ ] ]
[.$c(1-\alpha)^2\alpha n$
[.$\vdots$ ] ] ]
[.$c(1-\alpha)^2n$
[.$c(1-\alpha)^2\alpha n$
[.$\vdots$ ] ]
[.$c(1-\alpha)^3n$
[.$\vdots$ ] ] ] ] ]
\end{tikzpicture}
\end{minipage}
\begin{minipage}[b]{1.1\linewidth}
\centering
\begin{tikzpicture}[scale=.75,sibling distance=0pt]
\Tree [.$cn$
[.$cn$
[.$cn$
[.$cn$
[.$\vdots$ ] ] ] ] ]
\end{tikzpicture}
\end{minipage}
\end{figure}
\end{document}