Problem 4-3

More recurrence examples

Give asymptotic upper and lower bounds for $T(n)$ in each of the following recurrences. Assume that $T(n)$ is constant for sufficiently small $n$. Make your bounds as tight as possible, and justify your answers.

a. $T(n) = 4T(n/3) + n \lg n$.

$a = 4, b = 3$ and $f(n) = n \lg n$.

Case 1 of the Master Theorem applies since $f(n) = O(n^{\lg_3 4 - \epsilon}) = O(n^{1.26 - \epsilon}) \implies 0 < \epsilon < 0.26$. Thus the solution to the recurrence is $T(n) = \Theta(n^{\log_3 4})$.

b. $T(n) = 3T(n/3) + n / \lg n$.

$a = 3, b = 3$ and $f(n) = n / \lg n$.

Case 1 does not apply since $f(n) \neq O(n^{\log_3 3 - \epsilon}) = O(n^{1-\epsilon})$.

Case 2 does not apply since $f(n) \neq \Theta(n^{\log_3 3}) = \Theta(n)$.

Case 3 does not apply since $f(n) \neq \Omega(n^{\log_3 3 + \epsilon}) = \Omega(n^\epsilon)$

Because all three cases do not apply, we cannot apply the master method. The recurrence $T(n) = 3T(n/3) + n / \lg n$ has the following recursion tree:

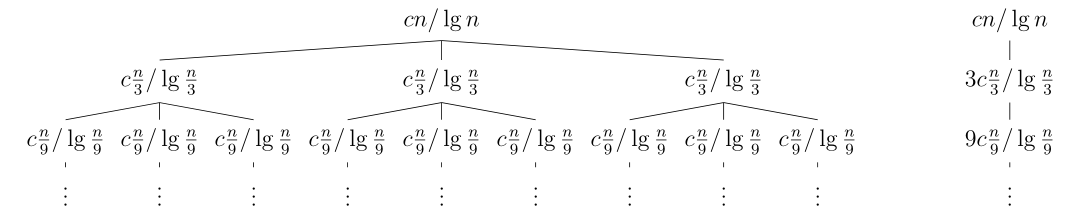
$4.3 Recursion Tree$

Adding up the costs of each level of the tree (utilizing the harmonic series identity):

\[\begin{split} T(n) & = cn /\lg n + 3c\frac{n}{3} /\lg \frac{n}{3} + 9c\frac{n}{9} /\lg \frac{n}{9} + \cdots + 3^{\log_3 n} c \frac{n}{3^{\log_3 n}} / \lg \frac{n}{3^{\log_3 n}} \\ & = \sum\limits_{i=0}^{\log_3 n - 1} 3^i c \frac{n}{3^i} / \lg \frac{n}{3^i} \\ & = \sum\limits_{i=0}^{\log_3 n - 1} cn / \lg \frac{n}{3^i} \\ & = cn \sum\limits_{i=0}^{\log_3 n - 1} 1 / \lg \frac{n}{3^i} \\ & = \Theta \left( cn \sum\limits_{i=0}^{\log_3 n - 1} 1 / \log_3 \frac{n}{3^i} \right) \\ & = \Theta \left( cn \sum\limits_{i=1}^{\log_3 n} \frac{1}{i} \right) \\ & = \Theta(n \lg \lg n) \\ \end{split}\]

The following LaTex code was used to generate the above recursion tree:

\documentclass[12pt]{article}
\usepackage{forest}
\usepackage{tikz-qtree}
\begin{document}

\begin{figure}
\begin{minipage}[b]{0.5\linewidth}
\centering
\begin{tikzpicture}[scale=.75,sibling distance=0pt]
\Tree [.$cn/\lg n$ 
        [.$c\frac{n}{3}/\lg \frac{n}{3}$ 
          [.$c\frac{n}{9}/\lg \frac{n}{9}$
            [.$\vdots$ ] ]
          [.$c\frac{n}{9}/\lg \frac{n}{9}$
            [.$\vdots$ ] ]
          [.$c\frac{n}{9}/\lg \frac{n}{9}$
            [.$\vdots$ ] ] ]
        [.$c\frac{n}{3}/\lg \frac{n}{3}$ 
          [.$c\frac{n}{9}/\lg \frac{n}{9}$
            [.$\vdots$ ] ]
          [.$c\frac{n}{9}/\lg \frac{n}{9}$
            [.$\vdots$ ] ]
          [.$c\frac{n}{9}/\lg \frac{n}{9}$
            [.$\vdots$ ] ] ]
        [.$c\frac{n}{3}/\lg \frac{n}{3}$ 
          [.$c\frac{n}{9}/\lg \frac{n}{9}$
            [.$\vdots$ ] ]
          [.$c\frac{n}{9}/\lg \frac{n}{9}$
            [.$\vdots$ ] ]
          [.$c\frac{n}{9}/\lg \frac{n}{9}$
            [.$\vdots$ ] ] ] ]
\end{tikzpicture}
\end{minipage}
\begin{minipage}[b]{.9\linewidth}
\centering
\begin{tikzpicture}[scale=.75,sibling distance=1pt]
\Tree [.$cn/\lg n$
        [.$3c\frac{n}{3}/\lg \frac{n}{3}$
          [.$9c\frac{n}{9}/\lg \frac{n}{9}$
            [.$\vdots$ ] ] ] ]
\end{tikzpicture}
\end{minipage}
\end{figure}
\end{document}

c. $T(n) = 4T(n/2) + n^2 \sqrt{n}$.

$a = 4, b = 2$ and $f(n) = n^2 \sqrt{n}$.

Case 1 does not apply since $f(n) \neq O(n^{\log_2 2 - \epsilon}) = O(n^{1 - \epsilon})$.

Case 2 does not apply since $f(n) \neq \Theta(n^{\log_2 2}) = \Theta(n)$.

Case 3 applies since $\Omega(n^{\log_2 2 + \epsilon }) = \Omega(n^{1+1})$ and

\[\begin{split} a(f(n/b)) & \leq cf(n) \\ 4(f(n/2)) & \leq cn^2 \sqrt{n} \\ 4\left(\frac{n}{2} \right)^2 \sqrt{\frac{n}{2}} & \leq cn^2\sqrt{n} \\ 4\left(\frac{n}{2}\right)^{2.5} & \leq cn^{2.5} \\ \end{split}\]

holds for $0 < c \lesssim 0.7$. Thus the solution to the recurrence is $T(n) = \Theta(n^2 \sqrt{n})$

d. $T(n) = 3T(n/3 - 2) + n/2$.

We do not need to care about the term being subtracted with sufficiently large values of $n$. Therefore we can consider the equivalent recurrence $T(n) = 3T(n/3) + n/2$ and apply the Master Theorem:

$a = 3, b = 3$ and $f(n) = n/2$.

Case 1 does not apply since $f(n) \neq O(n^{\log_3 3 - \epsilon}) = O(n^{-\epsilon})$.

Case 2 applies since $f(n) = \Theta(n^{\log_3 3}) = \Theta(n)$, and thus the solution to the recurrence is $T(n) = \Theta(n^{\log_3 3} \lg n) = \Theta(n \lg n)$.

e. $T(n) = 2T(n/2) + n / \lg n$.

Noting that this is the same recurrence as b. but with $a = 2$ and $b = 2$, it is clear that this lockstep change in terms will not result in a different conclusion. Therefore, the solution to this recurrence is $\Theta(n \lg \lg n)$.

f. $T(n) = T(n/2) + T(n/4) + T(n/8) + n$.

This tree would take ridiculous amounts of horizontal space to represent graphically, but the only real important thing to note is that it is not complete. For the levels that are complete (down to depth $\lg_8 n$) we have a cost of $\frac{1}{2}cn + \frac{1}{4}cn + \frac{1}{8}cn$. Thus the cost of the entire tree is at most:

\[\begin{split} T(n) & \leq \sum\limits_{i=0}^{\lg n - 1} \left( \frac{7}{8}\right)^i cn \\ & \leq cn \sum\limits_{i=0}^{\lg n - 1} \left( \frac{7}{8}\right)^i \\ & \leq cn \frac{\left(\frac{7}{8}\right)^{\lg n} - 1}{\frac{7}{8} - 1} \\ & \leq -cn \frac{1 - n^{\lg7 - 3}}{\frac{1}{8}} \\ & \leq 8cn - 8cn^{\lg 7 - 3} \\ & = O(n) \\ \end{split}\]

Based on this calculation we guess that $T(n) \leq cn$. Substituting this into the recurrence yields

\[\begin{split} T(n) & \leq \frac{cn}{2} + \frac{cn/4} + \frac{cn/8} + n \\ & = \frac{7}{8}cn + n \\ & \leq cn \\ \end{split}\]

Where the last step holds for $c \geq 8$.

g. $T(n) = T(n-1) + 1/n$.

Adding up the costs of each level of the tree (which is trivial to visualize):

\[\begin{split} T(n) &= \frac{1}{n} + \frac{1}{n-1} + \cdots + \frac{1}{1} \\ &= \sum\limits_{i=0}^{n - 1} \frac{1}{n - i} \\ &= \sum\limits_{i=1}^{n} \frac{1}{n} \\ &= \Theta(\lg n) \\ \end{split}\]

h. $T(n) = T(n - 1) + \lg n$.

\[\begin{split} T(n) &= \lg n + \lg (n-1) + \lg (n-2) \cdots + \lg 1 \\ &= \sum\limits_{i=1}^{n} \lg i \\ &= \lg n! \\ &\leq \lg n^n \\ &= \Theta(n \lg n) \\ \end{split}\]

i. $T(n) = T(n-2) + 1/\lg n$.

\[\begin{split} T(n) & = \frac{1}{\lg n} + \frac{1}{\lg (n -2)} + \frac{1}{\lg(n - 4)} + \cdots + 1\\ &= \sum\limits_{i=1}^{n/2} \frac{1}{\lg 2i}\\ &= \Theta\left(\frac{n}{\lg n}\right) \\ \end{split}\]

j. $T(n) = \sqrt{n}T (\sqrt{n}) + n$.

(Shamelessly relied entirely on the solutions manual for this esoteric problem) Let $i$ be the smallest $i$ so that $n^{\frac{1}{2^i}} < 2$. Recall from a previous problem (3-6.e) that this is $\lg \lg n$. Expanding the recurrence, we have that it is

\[\begin{split} T(n) &= n^{1 - \frac{1}{2^i}}T(2) + n + n \sum\limits_{j=1}^{i} \\ &= \Theta(n \lg \lg n) \\ \end{split}\]