Professor Bunyan thinks he has discovered a remarkable property of binary search trees. Suppose that the search for key \(k\) in a binary search tree ends up in a leaf. Consider three sets: \(A\), the keys to the left of the search path; \(B\), the keys on the search path; and \(C\), the keys to the right of the search path. Professor Bunyan claims that any three keys \(a \in A\), \(b \in B\), and \(c \in C\) must satisfy \(a \leq b \leq c\). Give a smallest possible counterexample to the professor’s claim.

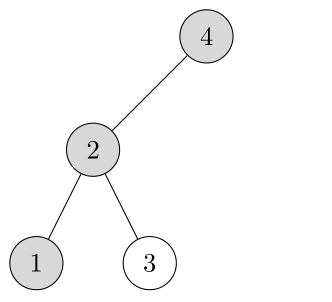
In this example, we are searching for key \(k = 1\) and the shaded nodes represent our path from root to leaf. This search path gives us \(A = \{\}\), \(B = \{4, 2, 1\}\) and \(C = \{3\}\). Because \(3 < 4\), Professor Bunyan’s claim that \(a \leq b \leq c\) does not hold.

The following LaTeX code was used to generate the above binary search tree:

\documentclass[border = 5pt, tikz]{standalone}

\begin{document}
\begin{tikzpicture}[
  every node/.style = {minimum width = 2em, draw, circle},
  shade/.style = {fill=black!15},
  level/.style = {sibling distance = 30mm/#1}
  ]
  \node [shade] {4}
  child {node [shade] {2}
        child {node [shade] {1}}
        child {node {3}}
        }
  child {edge from parent[draw = none]};
\end{tikzpicture}
\end{document}