Exercise 13.2-5

We say that a binary search tree $T_1$ can be right-converted to binary search tree $T_2$ if it is possible to obtain $T_2$ from $T_1$ via a series of calls to RIGHT-ROTATE. Give an example of two trees $T_1$ and $T_2$ such that $T_1$ cannot be right-converted to $T_2$. Then, show that if a tree $T_1$ can be right-converted to $T_2$, it can be right-converted using $O(n^2)$ calls to RIGHT-ROTATE.

Let $T_1$ be

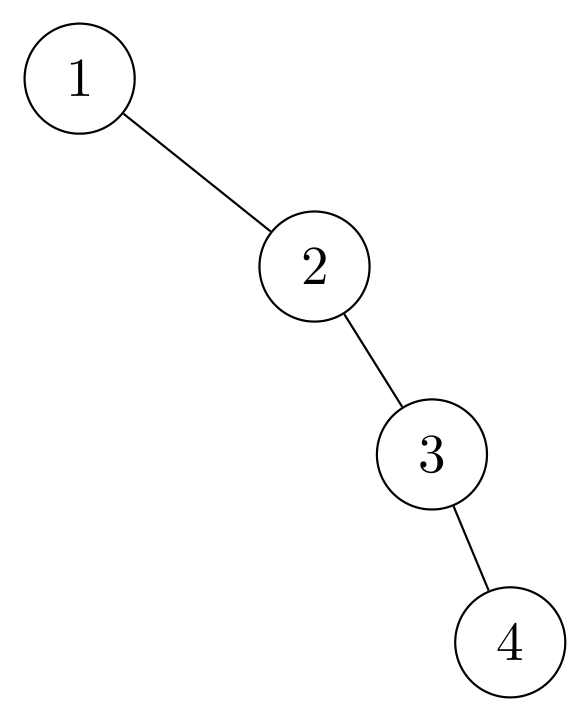
$13.2-5 T_1 Binary Search Tree$

and let $T_2$ be

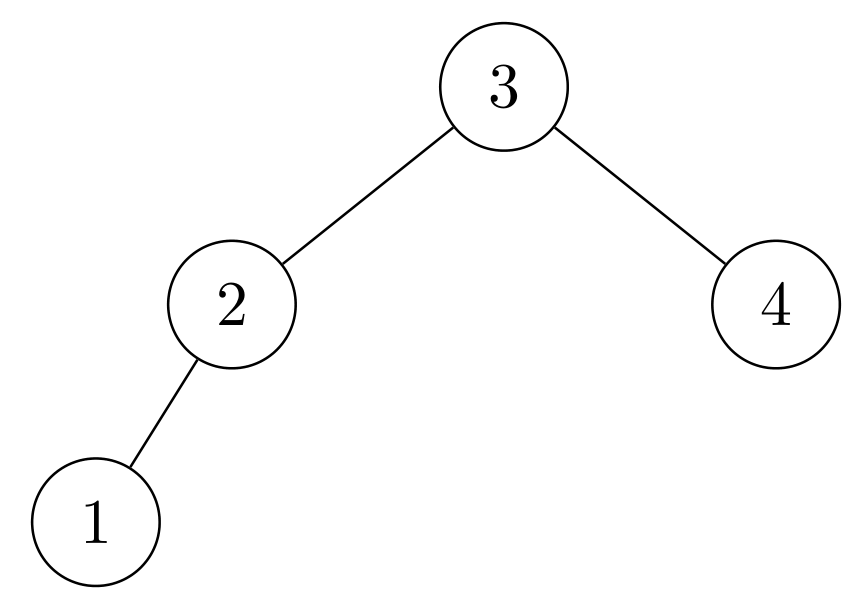
$13.2-5 T_2 Binary Search Tree$

First of all, we can see that both $T_1$ and $T_2$ satisfy the requirements of a Binary Search Tree (which, oddly enough, the actual solution manual fails to consider). Immediately we see that $T_1$ cannot be RIGHT-ROTATEd into $T_2$ because $T_1$ cannot be RIGHT-ROTATEd at all! The operation RIGHT-ROTATE($x$) requires that $x.\text{left} \neq NIL$ when in fact $x.\text{left} = NIL$ for all $x \in T_1$.

Next, consider a pair of binary search trees $T_1$ and $T_2$ where $T_1$ can be right-converted to $T_2$. By definition, $T_1$ and $T_2$ must have an identical inorder traversal, otherwise they could not be converted to one another. Therefore we know that both $T_1$ and $T_2$ share an identical set of keys and differ only in shape. At one extreme, we have the trivial case in which $T_1$ and $T_2$ also share a shape in which case they are equivalent.

What about the other extreme? In the worst case, $T_1$ is a left-skewed chain and $T_2$ is a balanced Binary Search Tree with the same inorder traversal. The RIGHT-ROTATE operation promotes a node up one depth-level every time it runs. The solution follows intuitively from this thought process, but let’s approach it a bit more formally.

Suppose that node $k$ is at depth $d_1(k)$ in $T_1$ and depth $d_2(k)$ in $T_2$. To get from depth $d_1(k)$ to depth $d_2(k)$, the node must move upward by $\Delta(k) = d_1(k) - d_2(k)$. Since RIGHT-ROTATE can move $k$ up by at most 1 level of depth, we know that node $k$ requires at most $\Delta(k)$ calls to RIGHT-ROTATE.

The total number of rotations required to transform $T_1$ into $T_2$ is then

\[\sum_k \Delta(k) = \sum_k (d_1(k) - d_2(k))\]

We know that $d_2(k)$ is always $\ge 0$ so the worst case is when $d_2(k)$ is 0:

\[\sum_k d_1(k)\]

This is the sum of the depths of the initial tree. In the worst-case we have a left-skewed BST of height $n$ with depths of $0, 1, 2, ..., n-1$. The sum of these depths is:

\[0 + 1 + 2 + \cdots + (n - 1) = \frac{n(n-1)}{2} = O(n^2)\]

Therefore:

\[\sum_k d_1(k) = O(n^2)\]

The following block of LaTeX code was used to generate $T_1$:

\documentclass[border = 5pt, tikz]{standalone}

\begin{document}
\begin{tikzpicture}[
  every node/.style = {minimum width = 2em, draw, circle},
  level distance = 12mm,
  level/.style = {sibling distance = 30mm/#1}
]
  \node {1}
    child [missing]
    child { node {2}
      child [missing]
      child { node {3}
        child [missing]
        child { node {4} }
      }
    };
\end{tikzpicture}
\end{document}

The following block of LaTeX code was used to generate $T_2$:

\documentclass[border = 5pt, tikz]{standalone}

\begin{document}
\begin{tikzpicture}[
  every node/.style = {minimum width = 2em, draw, circle},
  level distance = 12mm,
  level/.style = {sibling distance = 30mm/#1}
]
  \node {3}
    child { node {2}
      child { node {1} }
      child [missing]
    }
    child { node {4} };
\end{tikzpicture}
\end{document}