Give an adjacency-list representation for a complete binary tree on 7 vertices. Give an equivalent adjacency-matrix representation. Assume that vertices are numbered from 1 to 7 as in a binary heap.

For reference, this is the binary tree that I will be representing:

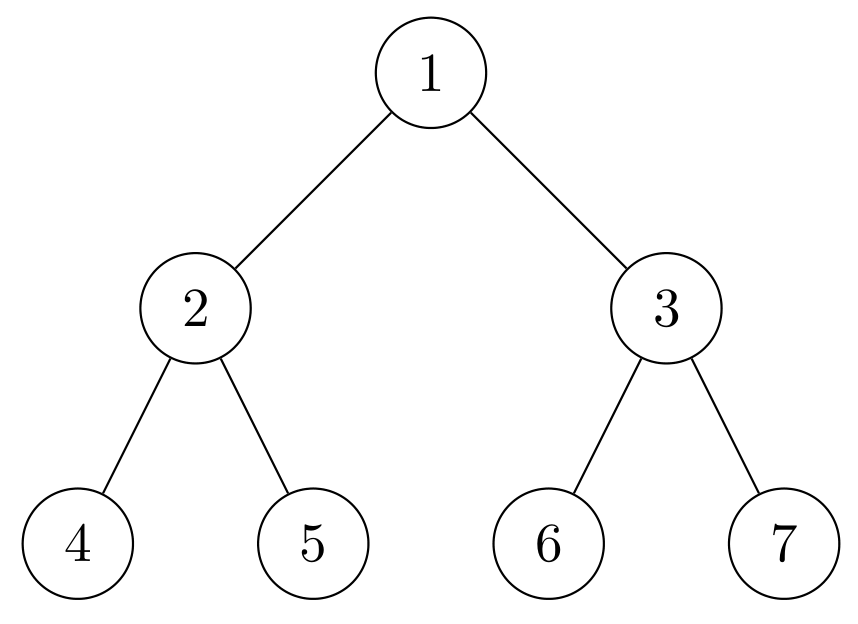
Adjacency-list representation:

\[\begin{align*} 1 &\rightarrow \boxed{2} \rightarrow \boxed{3} \\ 2 &\rightarrow \boxed{4} \rightarrow \boxed{5} \\ 3 &\rightarrow \boxed{6} \rightarrow \boxed{7} \\ 4 &\rightarrow \boxed{2} \\ 5 &\rightarrow \boxed{2} \\ 6 &\rightarrow \boxed{3} \\ 7 &\rightarrow \boxed{3} \end{align*}\]

Adjacency-matrix representation:

\[\begin{array}{c|ccccccc|} & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\ \hline 1 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ 2 & 1 & 0 & 0 & 1 & 1 & 0 & 0 \\ 3 & 1 & 0 & 0 & 0 & 0 & 1 & 1 \\ 4 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 5 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 6 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 7 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ \hline \end{array}\]

The following block of LaTeX code was used to generate the above binary tree:

\documentclass[border = 5pt, tikz]{standalone}

\begin{document}
\begin{tikzpicture}[
  every node/.style = {minimum width = 2em, draw, circle},
  level/.style = {sibling distance = 30mm/#1}
  ]
  \node {1}
  child {node {2}
        child {node {4}}
        child {node {5}}
        }
  child {node {3}
        child {node {6}}
        child {node {7}}
        };
\end{tikzpicture}
\end{document}