Use a recursion tree to determine a good asymptotic upper bound on the recurrence \(T(n) = T(n-1) + T(n/2) + n\). Use the substitution method to verify your answer.
The recurrence \(T(n) = T(n-1) + T(n/2) + n\) has the following recursion tree (Note however that this tree is not full as one path depletes \(n\) much quicker than the other)
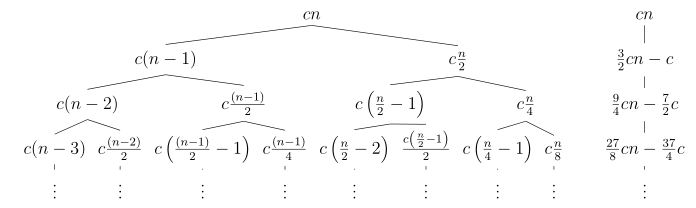
Summing the cost of the longest simple path from the root to a leaf is
\[\begin{split} \sum\limits_{i=0}^{n}c(n-i) & = c\sum\limits_{i=0}^{n}i \\ & = c \frac{n(n+1)}{2} \\ & = c \frac{n^2}{2} + \frac{c}{2} \\ & = O(n^2) \\ \end{split}\]This informs our guess for a lower bound: \(T(n) \geq cn^2\). Substituting this into the recurrence yields
\[\begin{split} T(n) & \geq c(n-1)^2 + c\left(\frac{n}{2}\right)^2 + n \\ & = cn^2 - 2cn + 1 + \frac{cn^2}{4} + n \\ & = \frac{5}{4}cn^2 - 2cn + n + 1 \\ & \geq cn^2 \\ \end{split}\]Where the last step holds for all \(c \geq 1\). Thus we have \(T(n) = \Omega(n^2)\).
Our recursion tree doesn’t provide any obvious insight into an upper bound. But consider a similar recurrence
\[S(n) = 2T(n-1) + n\]which is similar to \(T(n)\) but is more costly. We know that \(S(n) = O(2^n)\) so a reasonable guess for our unique recurrence \(T(n)\) would be \(T(n) \leq c2^n - bn\). Substituting this into the recurrence yields
\[\begin{split} T(n) & \leq 2(c2^{n-1} - b(n - 1)) + n \\ & = c2^n - 2bn + 2b + n \\ & = c2^n - bn - n(b - 1) + 2b \\ & \leq c2^n - bn \\ \end{split}\]Where the last step holds for \(b \geq 3\). Therefore we have \(T(n) = O(2^n)\).
The following LaTeX code was used to generate the above recursion tree:
\documentclass[12pt]{article}
\usepackage{forest}
\usepackage{tikz-qtree}
\begin{document}
\begin{figure}
\begin{minipage}[b]{0.5\linewidth}
\centering
\begin{tikzpicture}[scale=.75,sibling distance=0pt]
\Tree [.$cn$
[.$c(n-1)$
[.$c(n-2)$
[.$c(n-3)$
[.$\vdots$ ] ]
[.$c\frac{(n-2)}{2}$
[.$\vdots$ ] ] ]
[.$c\frac{(n-1)}{2}$
[.$c\left(\frac{(n-1)}{2}-1\right)$
[.$\vdots$ ] ]
[.$c\frac{(n-1)}{4}$
[.$\vdots$ ] ] ] ]
[.$c\frac{n}{2}$
[.$c\left(\frac{n}{2}-1\right)$
[.$c\left(\frac{n}{2}-2\right)$
[.$\vdots$ ] ]
[.$\frac{c\left(\frac{n}{2}-1\right)}{2}$
[.$\vdots$ ] ] ]
[.$c\frac{n}{4}$
[.$c\left(\frac{n}{4}-1\right)$
[.$\vdots$ ] ]
[.$c\frac{n}{8}$
[.$\vdots$ ] ] ] ] ]
\end{tikzpicture}
\end{minipage}
\begin{minipage}[b]{.6\linewidth}
\centering
\begin{tikzpicture}[scale=.75,sibling distance=0pt]
\Tree [.$cn$
[.$\frac{3}{2}cn-c$
[.$\frac{9}{4}cn-\frac{7}{2}c$
[.$\frac{27}{8}cn-\frac{37}{4}c$
[.$\vdots$ ] ] ] ] ]
\end{tikzpicture}
\end{minipage}
\end{figure}
\end{document}