Argue that the solution to the recurrence \(T(n) = T(n/3) + T(2n/3) + cn\), where \(c\) is a constant, is \(\Omega(n \lg n)\) by appealing to a recursion tree.

The recurrence \(T(n) = T(n/3) + T(2n/3) + cn\) has the following recursion tree (Note that this is identical to figure 4.6 in the text)

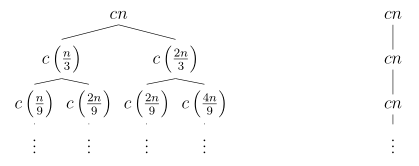
The shortest simple path from the root to a leaf is \(n \rightarrow (1/3)n \rightarrow (1/3)^2n \rightarrow \cdots \rightarrow 1\). Since \((1/3)^kn = 1\) when \(k = \log_{3}n\), this path has length \(\log_{3}n\). Thus the cost of the algorithm is

\[cn(\log_{3}n + 1) \geq cn \log_{3} n = \frac{c}{\log_{3}}n \log n = \Omega(n \log n)\]