Draw a recursion tree for \(T(n) = 4T(\lfloor n/2 \rfloor) + cn\), where \(c\) is a constant, and provide a tight asymptotic bound on its solution. Verify your bound by the substitution method.
The recurrence \(T(n) = 4T(\lfloor n/2 \rfloor) + cn\) has the following recursion tree:
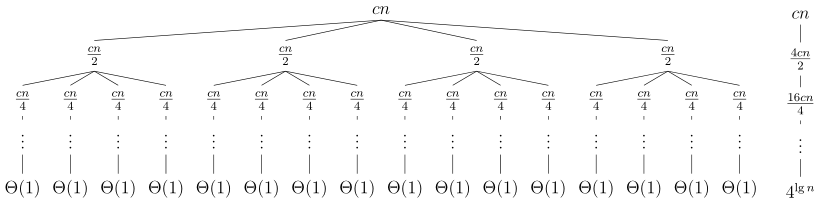
Adding up the costs of each level of the tree:
\[\begin{split} T(n) & = cn + 2cn + 4cn + \cdots + \Theta(n^2) \\ & = \sum\limits_{i=0}^{\lg(n-1)} 2^icn + \Theta(n^2) \\ & = \frac{2^{\lg n} - 1}{2 - 1}cn + \Theta(n^2) \\ & = \Theta(n^2) \\ \end{split}\]In order to produce a tight asymptotic bound, we first guess that \(T(n) \leq bn^2 - cn\) in order to show that \(T(n) = O(n^2)\). Substituting this into the recurrence yields
\[\begin{split} T(n) & \leq 4b(n/2)^2 - 4c(n/2) + cn \\ & = bn^2 - 2cn + cn \\ & = bn^2 - cn \\ & \leq bn^2 - cn \end{split}\]Where the last step holds for all \(b > 0\). Next we guess that \(T(n) \geq bn^2 - cn\) in order to show that \(T(n) = \Omega(n^2)\). Substituting this into the recurrence yields
\[\begin{split} T(n) & \geq 4b(n/2)^2 - 4c(n/2) + cn \\ & = bn^2 - 2cn + cn \\ & = bn^2 - cn \\ & \geq bn^2 - cn \end{split}\]Where the last step holds for all \(b > 0\). Therefore \(T(n) = \Theta(n^2)\).
The following LaTeX code was used to generate the above recursion tree:
\documentclass[12pt]{article}
\usepackage{forest}
\usepackage{tikz-qtree}
\begin{document}
\begin{figure}
\begin{minipage}[b]{0.5\linewidth}
\centering
\begin{tikzpicture}[scale=.75,sibling distance=0pt]
\Tree [.$cn$
[.$\frac{cn}{2}$
[.$\frac{cn}{4}$
[.$\vdots$
[.$\Theta(1)$ ] ] ]
[.$\frac{cn}{4}$
[.$\vdots$
[.$\Theta(1)$ ] ] ]
[.$\frac{cn}{4}$
[.$\vdots$
[.$\Theta(1)$ ] ] ]
[.$\frac{cn}{4}$
[.$\vdots$
[.$\Theta(1)$ ] ] ] ]
[.$\frac{cn}{2}$
[.$\frac{cn}{4}$
[.$\vdots$
[.$\Theta(1)$ ] ] ]
[.$\frac{cn}{4}$
[.$\vdots$
[.$\Theta(1)$ ] ] ]
[.$\frac{cn}{4}$
[.$\vdots$
[.$\Theta(1)$ ] ] ]
[.$\frac{cn}{4}$
[.$\vdots$
[.$\Theta(1)$ ] ] ] ]
[.$\frac{cn}{2}$
[.$\frac{cn}{4}$
[.$\vdots$
[.$\Theta(1)$ ] ] ]
[.$\frac{cn}{4}$
[.$\vdots$
[.$\Theta(1)$ ] ] ]
[.$\frac{cn}{4}$
[.$\vdots$
[.$\Theta(1)$ ] ] ]
[.$\frac{cn}{4}$
[.$\vdots$
[.$\Theta(1)$ ] ] ] ]
[.$\frac{cn}{2}$
[.$\frac{cn}{4}$
[.$\vdots$
[.$\Theta(1)$ ] ] ]
[.$\frac{cn}{4}$
[.$\vdots$
[.$\Theta(1)$ ] ] ]
[.$\frac{cn}{4}$
[.$\vdots$
[.$\Theta(1)$ ] ] ]
[.$\frac{cn}{4}$
[.$\vdots$
[.$\Theta(1)$ ] ] ] ] ]
\end{tikzpicture}
\end{minipage}
\begin{minipage}[b]{1.05\linewidth}
\centering
\begin{tikzpicture}[scale=.75,sibling distance=0pt]
\Tree [.$cn$
[.$\frac{4cn}{2}$
[.$\frac{16cn}{4}$
[.$\vdots$
[.$4^{\lg n}$ ] ] ] ] ]
\end{tikzpicture}
\end{minipage}
\end{figure}
\end{document}