Can the master method be applied to the recurrence \(T(n) = 4T(n/2) + n^2 \lg n\)? Why or why not? Give an asymptotic upper bound for this recurrence.

\(a = 4\), \(b = 2\) and \(f(n) = n^2 \lg n\).

Case 1 does not apply since \(f(n) \neq O(n^{\log_{2}4 - \epsilon}) = O(n^{2 - \epsilon})\).

Case 2 does not apply since \(f(n) \neq \Theta(n^{\log_{2}4}) = \Theta(n^2)\).

Case 3 does not apply since \(f(n) \neq \Omega(n^{\log_{2}4 + \epsilon}) = \Omega(n^{2 + \epsilon})\).

Because all three cases do not apply, we cannot apply the master method. The recurrence \(T(n) = 4T(n/2) + n^2 \lg n\) has the following recursion tree (truncated because splitting into 4 different large terms isn’t a great look):

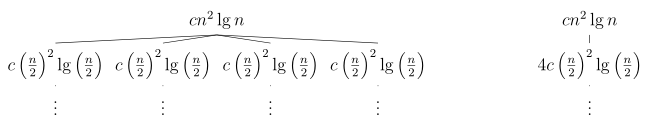
Adding up the costs of each level of the tree:

\[\begin{split} T(n) & = cn^2 \lg n + 4c\left(\frac{n}{2}\right)^2 \lg \left(\frac{n}{2}\right) + 16c\left(\frac{n}{4}\right)^2 \lg \left(\frac{n}{4}\right) + \cdots + 4^{\lg n}c \left(\frac{n}{2^{\lg n}}\right)^2 \lg \left(\frac{n}{2^{\lg n}}\right) \\ & = \sum\limits_{i=0}^{\lg n} 4^{i}c \left( \left( \frac{n}{2^i} \right)^2 \lg \frac{n}{2^i} \right) \\ & = \sum\limits_{i=0}^{\lg n} 4^{i}c \left( \frac{n^2(\lg n - \lg 2^i)}{2^{2i}}\right) \\ & = cn^2 \sum\limits_{i=0}^{\lg n} (\lg n - \lg 2^i) \\ & = cn^2 \left( \sum\limits_{i=0}^{\lg n} \lg n - \sum\limits_{i=0}^{\lg n} i \right) \\ & = cn^2 \left(\lg n \lg n - \frac{\lg n (\lg n + 1)}{2} \right) \\ & = cn^2 \left( \frac{(\lg n)^2}{2} - \frac{ \lg n}{2} \right) \\ & \leq cn^2 \frac{(\lg n)^2}{2} \\ & \leq cn^2(\lg n)^2 \\ & = O(cn^2 \lg^2 n) \\ \end{split}\]

Based on this calculation we guess that \(T(n) \leq cn^2 \lg^2 n\). Substituting this into the recurrence yields

\[\begin{split} T(n) & \leq 4c \left( \left( \frac{n}{2} \right)^2 \lg^2 \left( \frac{n}{2} \right) \right) + n^2 \lg n \\ & = 4c \left( \frac{n^2}{4} \lg \left(\frac{n}{2}\right) \lg \left(\frac{n}{2}\right) \right) + n^2 \lg n \\ & = cn^2 \lg \left( \frac{n}{2} \right) \lg \left( \frac{n}{2} \right) + n^2 \lg n \\ & = cn^2 \lg \left(\frac{n}{2} \right) \lg n - cn^2 \lg \left(\frac{n}{2} \right) + n^2 \lg n \\ & = cn^2 \lg^2 n - cn^2 \lg n - cn^2 \lg n + cn^2 + n^2 \lg n \\ & \leq cn^2 \lg^2 n \\ \end{split}\]

Where the last step holds for \(c \geq 1\).

The following LaTex code was used to generate the above recursion tree:

\documentclass[12pt]{article}
\usepackage{forest}
\usepackage{tikz-qtree}
\begin{document}

\begin{figure}
\begin{minipage}[b]{0.5\linewidth}
\centering
\begin{tikzpicture}[scale=.75,sibling distance=0pt]
\Tree [.$cn^2\lg n$ 
        [.$c\left(\frac{n}{2}\right)^2\lg \left(\frac{n}{2}\right)$ 
          [.$\vdots$ ] ]
        [.$c\left(\frac{n}{2}\right)^2\lg \left(\frac{n}{2}\right)$ 
          [.$\vdots$ ] ] 
        [.$c\left(\frac{n}{2}\right)^2\lg \left(\frac{n}{2}\right)$
          [.$\vdots$ ] ] 
        [.$c\left(\frac{n}{2}\right)^2\lg \left(\frac{n}{2}\right)$ 
          [.$\vdots$ ] ] ] ]
\end{tikzpicture}
\end{minipage}
\begin{minipage}[b]{.5\linewidth}
\centering
\begin{tikzpicture}[scale=.75,sibling distance=0pt]
\Tree [.$cn^2\lg n$
        [.$4c\left(\frac{n}{2}\right)^2\lg \left(\frac{n}{2}\right)$
          [.$\vdots$ ] ] ]
\end{tikzpicture}
\end{minipage}
\end{figure}
\end{document}