Consider the regularity condition \(af(n/b) \leq cf(n)\) for some constant \(c < 1\), which is part of case 3 of the master theorem. Give an example of constants \(a \leq 1\) and \(b > 1\) and a function \(f(n)\) that satisfies all the conditions in case 3 of the master theorem except the regularity condition.

Setting \(a = 1\) and \(b = 2\) gives us the convenient case where our \(f(n)\) must be \(\Omega(n^{\log_{2}1 + \epsilon}) = \Omega(n^{0+\epsilon})\). By selecting \(f(n) = n(2- \cos n)\) we are able to satisfy this condition for some \(\epsilon < 1\) and our \(f(n)\) has a graph that looks like this:

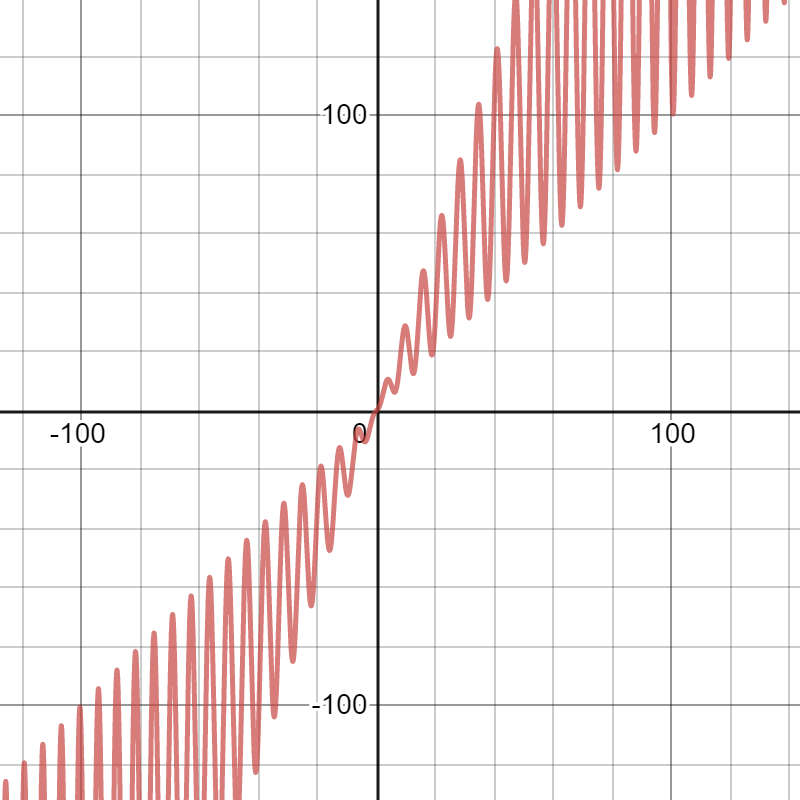
The regularity condition requires that for some constant \(c < 1\) and all sufficiently large \(n\) that:

\[\begin{split} af(n/b) & \leq cf(n) \\ 1 \cdot \frac{n}{2}\left(2 - \cos \frac{n}{2}\right) & \leq cn(2- \cos n) \\ 2 - \cos \frac{n}{2} & \leq 2c(2 - \cos n) \\ 2 - \cos \frac{n}{2} & \leq c(4 - 2 \cos n) \\ \frac{2- \cos \frac{n}{2}}{4 - \cos n} & \leq c \\ \end{split}\]

The graph of \(\frac{2- \cos \frac{n}{2}}{4 - \cos n}\) continues in a repeating pattern indefinitely. This pattern regularly exceeds \(1\) which means there is no valid value of \(c\) that satisfies this inequality for sufficiently large values of \(n\).